第五周将学习Grover算法
官方笔记我放在最后
Grover’s Algorithm
Intro
第一个问题, 量子计算机一定比经典计算机好吗?
不一定, 见最后一节
第二个问题, 量子计算机能有效的解决所有NP问题吗?
能, 就是我们将要学习的Grover算法
电话簿(phone book problem)
如果我们要通过电话查找人名(即在未排序的数据)中找到(暴力破解 brute force search)需要$O(n)$时间
旅行者问题(traveling salesman problem)
暴力破解找路径需要$O(n!)$
提出问题
对于旅行者问题问题, 你可能可以根据图的信息对暴力破解做一些优化, 但对于电话簿问题, 暴力破解没有任何可以优化的地方
如果你有办法使电话簿的暴力破解变简单, 那么你就能简化任何可以被暴力破解解决的问题中的暴力破解这一步(if you can simplify this brute force search which is applicable to the phone book problem, then you will simplify the brute force search for any problem which is solvable with the brute force search)
对于一个未知函数$f(a)=b$, 我们需要根据$b$找到$a$, 使用量子计算机可以加速暴力破解过程
Grover’s Algorithm. A Closer Look
为什么把初始状态弄成$s$?
因为$s$蕴含了所有的可能性
如果我们有多个$\omega$会怎么样?
我们必须精确的知道具体有多少个, 并以此来计算迭代数
如果我们不知道有几个, 那么我们有可能会过头或不到, 那么测量得到正确结果的可能性会降低
为什么我们选择$U_s$?
we need some point, some vector to reflect it in the desired direction, but we don’t know which direction is desired
说白了就是只知道这些信息, 所以只能这样
考虑一件事, 如果我们知道正好45度右上角的向量, 那么我们可以只需一次迭代
对于一个需要12次迭代的来说, 这个向量就是$s_6$, 同理$s_6$可以由$s$关于$s_3$对称直接得到, 这可以将算法的时间复杂度从$O(\sqrt{N})$优化为$O(\log_2 N)$(实现了量子计算机的指数级加速)
为了实现上面所说的, 我们需要一个叫做von neumann architecture的东西, 但这个东西仍是个问题(is still under the question)
另外, Grover算法被证明是最优的搜索算法, 下一节会讨论这个
Grover’s Algorithm Optimality
part1
我们能设计一个更优的算法吗?
Lov Grover证明了不可能, 换言之, Grover算法是最优的了
如果我们能找到满足(2)的$\mid \phi\rangle$, 那么(3)也将满足, 从而证明至少需要$O(\sqrt{N})$(即其他方法的时间复杂度一定大于等于$O(\sqrt{N})$, 而Grover算法的时间复杂度就是$O(\sqrt{N})$, 即为最优)
对于不同的正交的$\omega$, 经过迭代后的最终的$\phi_\omega$我们将他们也近似的看作是正交的, since the algorithm is so effective
我的理解是最终的误差($\phi_\omega$与$\omega$的角度)一定是小于等于$\theta$, 而
$$sin\theta = \frac{1}{2^{n/2}}$$
当$n$很大时, 这个夹角会很小, 即
$$\lim_{n\to \infty}\theta =0$$
part2
无
part3
md视频看完了告诉我这整个视频是错的, pdf过程也是错的正确证明过程如下, E和f定义没变
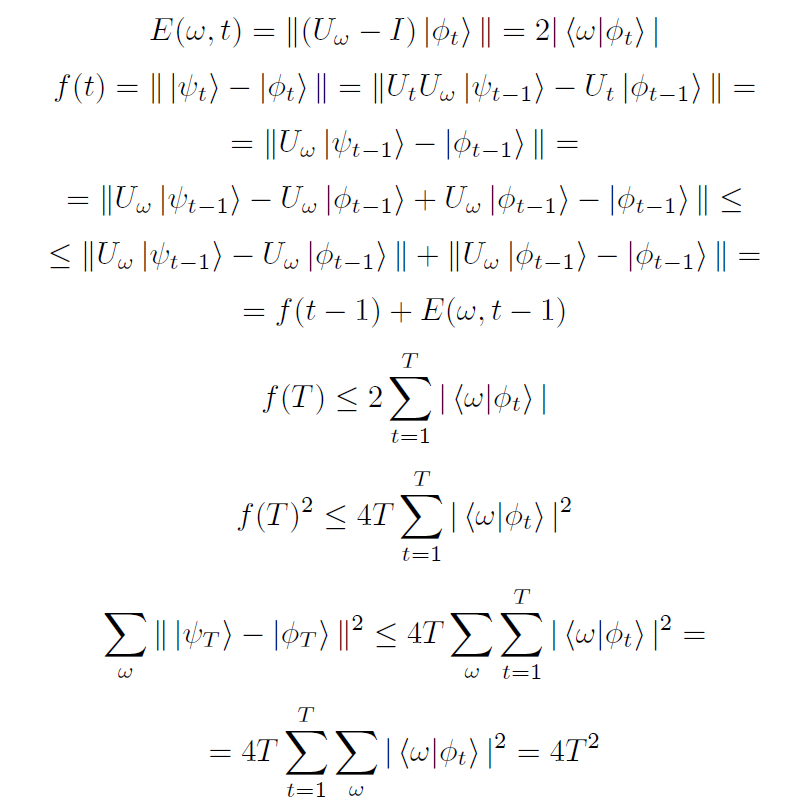
Quantum Computer Application Boundaries
看不懂
结论回答了第一个问题
在文中新构造的问题上, 量子计算机不可能比经典计算机快一倍以上
即, 量子计算机不是万能的
自己笔记
第一页
笔记中的 ∃! 表示只存在一个
$f_\omega(x)=\delta_{x=\omega}$意味着当$x=\omega$时, 右边为1, $x \neq \omega$时右边为0
$U_\omega$变换相当于超平面(hyperplane)对称
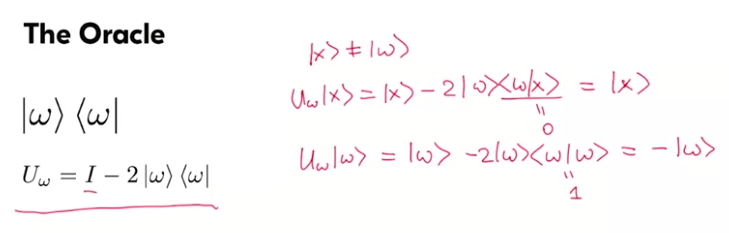
$U_s$变换相当于关于$s$对称
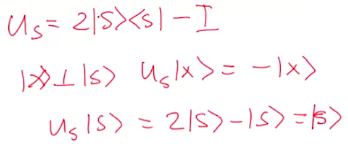
Each Grover’s iteration rotates the system in the direction $\mid\omega\rangle$ by the angle $2\theta$
第二页
在官方笔记图1中,垂直轴为我们要求的向量,水平轴是其余向量组成的超平面,因为初始状态$s$含有所有可能的向量,所以有一个微小的夹角
1.2开始定义一些新的符号, 对于2, 即定义了新的操作$U_t$, 当$t=s$时, 即$U_s$
对于(4), 前两项为单位向量
第五页
(9)和最后一行直接删掉的东西都是unitary
官方笔记
